Trigonometry was taught strangely in school. It seemed to jump right in with memorizing new ideas without first grounding the students in how to relate these concepts to anything that seems to matter.
A Strange Start for Trigonometry
One of the first things a student is asked to memorize is SOHCAHTOA (which our high school trigonometry teacher pronounced as a single four-syllabel word and told us to think of as the name of some Native American princess). SOHCAHTOA, of course, stands for the following three formulas:
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
These formulas referred to how to find these values in a very limited scenario where we are interested in a right triangle, that is, a triangle where one of the angles is 90 degrees.
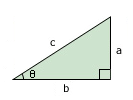 |
| A right triangle |
Sine, cosine and tangent, simply seem to be three different ratios that are defined to relate an angle on a right triangle (represented by the Greek letter θ) with the various sides of the triangle. In our picture, sin(θ) equals a/c; cos(θ) equals b/c; and tan(θ) equals a/b.
What does this have to do with anything? Why are we so interested in right triangles? Why not isosceles triangles?
Conversions Between Coordinate Systems
Trigonometry shouldn’t be thought of as being about ratios of sides of a right triangle. The more fundamental concept to trigonometry is that we’re talking about conversions between different coordinate systems.
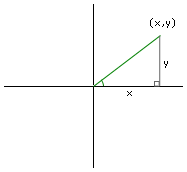 |
| Cartesian Coordinate System |
Students learning trigonometry are all familiar with the Cartesian coordinate system already. They know that a point in this coordinate system is designated by its x and y coordinate. This coordinate system is useful for many purposes, but is there another way to locate the point in space?
Sure. Consider a line that extends from (0, 0) to our point. We can call the length of this line r, and we can say θ represents the angle between the line and the positive x axis. The values r and θ give us a different way of representing the same point.
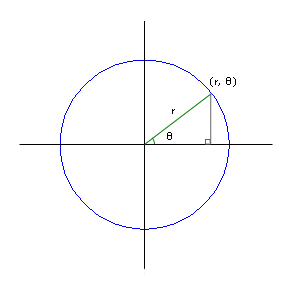 |
| Angular Coordinate System |
It’s the same point in space; it just is represented in a different coordinate system.
There has to be a relationship between the two coordinate systems though. They both have ways of representing the same point. So how are r and θ related to x and y? We simply define two new functions. One of them is called sine, the other cosine.
We’ll say that the y coordinate of the point equals r * sin(θ). The x coordinate equals r * cos(θ). That’s all that sine and cosine are — functions that have been defined to help translate from one coordinate system to another. These definitions for sine and cosine are completely equivalent to the definitions in SOHCAHTOA.
Where Does Pi Fit In?
People who recall their trigonometry undoubtedly wonder where π fits into the picture. We understand now how sine and cosine are used to convert from one coordinate system to another, but wasn’t there something about π?
Yes. The whole business about π was just about talking about another way of describing angles. We understand what 45o means. We understand a 90o angle. Where does π fit in?Let’s consider a circle where the radius, r, equals 1 (this circle is also called a unit circle). What is the circumference of the circle? The formula is c = 2πr. Since r equals 1, our circumference is 2π. 2π represents going the entire way around the circle and ending up back where we started. How long is the curve for a quarter of the circle? It’s 2π/4 or π/2. This means that somehow on a unit circle π/2 and 90o are related.
What is this relationship? All we’re talking about is a relationship between the angle θ and how far around the arc of the circle we go. The distance around the circle is what is known as the arc length. If we use the unit circle as a standard of measurement, we can say that an angle can be represented equally well in terms of degrees or arc length. That’s all. Nothing special.So why do we bother with arc length instead of degrees? No idea. Our guess is that it is simpler to manipulate π, which represents halfway around the circle, than 180o. The numbers are just easier to work with. Three quarters of a circle? 3π/2 — it’s easier than 270o.
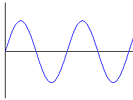
And Wasn’t Sine That Weird Wave?
When we think of sine, we think of a wave that goes up an down. What does this graph have to do with the coordinate systems we talked about?
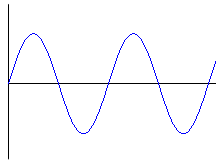 |
| Sine Wave |
This graph represents the value of sin(θ) as θ increases. The horizontal axis is θ; the vertical axis is sin(θ). To understand why it draws this graph let’s think about what happens as θ increases. We aren’t talking about r anywhere in here. Let’s just assume r stays constant. As θ increases and r remains constant, we trace a circle. What happens to sin(θ) as θ increases? We know sin(θ) equals y/r. With r constant, we find that sin(θ) is proportional to just y. Let’s think about what happens to y as θ increases (and we trace our way around a circle), so that we can draw our graph for sin(θ).
When θ is zero (that is, the angle between our point on the circle and the positive X axis is zero), our y coordinate is zero. As we go around the circle and θ increases from 0o to 90o, y increases sharply, then slows down towards the top. As θ continues to go from 90o to 180o, y drops back down until we reach zero again. As θ goes from 180o to 270o, y drops below the axis — first quickly, then it slows down as we reach 270o. Finally, as θ goes from 270o to 360o, y slowly increases until it reaches zero again. This description of what happens to y exactly traces out the sine wave we see in the graph. It repeats over and over because each time θ makes a complete revolution around the circle, we’ve returned back to our starting point.
So, What Should We Memorize?
There are actually a number of things to memorize in trigonometry. This web page cannot do justice to all of trigonometry, so we’ll leave with just a few values of sine and cosine that show up on almost every trigonometry test. The values of sine and cosine are typically hard to figure out and one usually needs either a chart or a calculator to find their values, but five angles in particular show up over and over: 0o, 30o, 45o, 60o and 90o. There is a mnemonic for remembering the values for sine and cosine. First, let’s look at a table showing their values:
| θ | sin(θ) | cos(θ) |
| 0o | 0 | 1 |
| 30o | 1/2 | sqrt(3)/2 |
| 45o | sqrt(2)/2 | sqrt(2)/2 |
| 60o | sqrt(3)/2 | 1/2 |
| 90o | 1 | 0 |
So, what’s the mnemonic? If you look down the column for sine, the values are equal to the square root of 0, 1, 2, 3, 4, each divided by 2 (e.g., sin(90o) = sqrt(4)/2 = 2/2 = 1). If you look down the column for cosine, the values are equal to the square root of 4, 3, 2, 1, 0, each again divided by 2.A 45o angle is obviously important, but what’s so important about 30o and 60o? Frank Lloyd Wright built all of his houses at a 30o angle with the east-west line so that, in his opinion, one would get the optimum amount of light from the windows throughout the day.
Putting It To Use
We were asked recently for the value of sin(16π/3) without using a calculator (for someone’s homework problem — not a real world example). How would we solve it? Well, we know that 2π is once around the circle and we end up back at our starting point. We can think of sin(16π/3) as sin(2π + 2π + 4π/3). The first two times around the circle we can just ignore. This means that sin(16π/3) = sin(4π/3). sin(4π/3) is half way around the circle, and then π/3 more. This means that we’re really interested in the value of sine for an angle drops down into the negative area of y axis by π/3 or 60o. From memory, we should know that sin(60o) is sqrt(3)/2, and since this is in the negative y area of the circle, we know that the value has to be negative. The answer is sin(16π/3) = -sqrt(3)/2.